Although in everyday life, near enough may be good enough, working with exact quantities can enable learners to experience the real power of mathematics, says Colin Foster…
Absolute precision is an aspect of learning mathematics that marks it out as different from any other subject. In this lesson, students use Pythagoras’ theorem to find accurate values for the perimeters of some triangles. Although the values of the perimeters are so close that it would be very hard to distinguish them by measurement, mathematics makes it possible to be absolutely sure about the order in which they come.
Perimeter refers to the distance all the way around the edge of a shape, so for any one of these triangles it is the sum of the lengths of the three sides. Q: Which one do you think has the biggest perimeter? Why? Which one has the smallest? Could you put them in order of how big their perimeters are? Learners could discuss this in pairs. If they have access to mini-whiteboards, they could list the order that they think is right; e.g., A < B < C < D < E < F.
Q: Who is confident about their order? Can you give a reason?
It is likely that learners will have very different orders at this stage. They will probably be judging by eye and it should be too difficult for them to be sure that way. If they start arguing about it, that is good, because the rest of the lesson will allow them to resolve the issue.
STARTER ACTIVITY
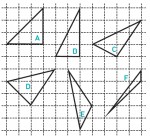
Q: Look at these triangles. Can you explain what mathematicians mean by the word ‘perimeter’?
MAIN ACTIVITIES
MEASURING PERIMETERS
Give learners some squared paper so that they can draw these triangles accurately. (Alternatively, you could photocopy them onto paper for them. If you do, try to make sure that the squares on the photocopy come out accurately as centimetre squares.) Q: Can you measure the perimeters and find out which one is the biggest, which one is the next biggest, and so on? Learners will need to measure carefully, and add up their three measurements for each triangle (perhaps using a calculator). It is very unlikely that they will agree about the order. The error involved in making their measurements is almost certainly going to be greater than the differences in the actual perimeters. Some learners may think that all the perimeters are the same. If so, you could ask: Q: Can you be sure that they are exactly the same, or are the differences just too small for you to measure?
CALCULATING PERIMETERS
How could we work out the perimeter of one of these triangles exactly? In A, the hypotenuse is 3 2 and in B it is 2 5, so the perimeters are:
| TRIANGLE | PERIMETER |
| A | 6+3 2 = 10.234 (3 dp) |
| B | 6+2 5 = 10.472 (3 dp) |
These values should tally approximately with the measurements that learners made earlier, but this time they can distinguish that B has a slightly larger perimeter than A, which they probably couldn’t determine before. Learners may be fine now to continue on their own and work out the perimeters of all of the other triangles. However, triangles C-F are harder. In triangle F, one of the sides is clearly 1 unit, and learners might notice that one of the other sides is the same as the hypotenuse in A, but the third side (and many of the sides in the other triangles) needs to be calculated using Pythagoras’ theorem. If learners are unsure how to do this, then it could be helpful to do triangle C together:
Choose a side for us to work out first. (e.g., the one marked in red below)
We can see this as the hypotenuse of a 2-by-1 rightangled triangle, so its length must be 22 + 12 = 5. Learners may notice that one of the other sides is clearly twice as long as this side, since 4-along-2-up is just twice as much as 2-along-1-up, so its length must be 2 5 (an even better shortcut is to notice that we have just calculated this same side, in a different orientation, in triangle B!) The remaining side in triangle C needs calculating, and comes to 13 , giving the perimeter as:
| TRIANGLE | PERIMETER |
| C | 3 5 + 13 = 10.314 (3 dp) |
So this triangle comes in between triangles A and B in perimeter. Now learners can find the perimeters of the remaining triangles D, E and F. They may be able to save time by noticing when a side in one triangle reappears (perhaps in a different orientation or scaled by a certain amount) in another triangle. For example, the 13 side in triangle C appears again in triangles D and E.
The answers are given below:
| TRIANGLE | PERIMETER |
| D | 2 2 + 13 + 17 = 10.557 (3 dp) |
| E | 5 + 13 + 26 = 10.941 (3 dp) |
| F | 6+3 2 = 10.243 (3 dp) |
So we have the order A = F < C < B < D < E. By calculating, we can see that triangles A and F have exactly the same perimeter. We could never know that they were exactly the same by measuring. Some learners may prefer to give their answers in centimetres, since perimeter is a length, but here the squares are just treated as arbitrary units.
When learners finish, their task is to draw some more triangles, where each vertex lies on a grid point, that have perimeters as near to these ones as they can. Some trial and error will be needed. Learners can judge by eye if they think the perimeter will be about right, and then calculate and see where it comes. Who can get the closest to these ones?
INVENTING TRIANGLES
You could conclude the lesson with a plenary in which learners talk about which of the triangles they found easier or harder to calculate, and why. They could also share any created triangles, and other learners could try to find where they fit into the ordering of A to F.
ADDITIONAL RESOURCES
IF YOU HAVE GEOBOARDS (OR COULD BUY SOME), THEN THERE ARE MANY INTERESTING TASKS RELATED TO THIS ONE THAT LEARNERS COULD TRY. THERE ARE LOTS OF IDEAS IN 100+ IDEAS FOR TEACHING MATHEMATICS, BY MIKE OLLERTON (2007, 2ND ED., CONTINUUM), AND IN THE ATM PUBLICATION USING GEOBOARDS (1992, ATM), AVAILABLE AT TINYURL.COM/TSGEOBOARD.
STRETCH THEM FURTHER
CONFIDENT LEARNERS COULD TRY TO INVENT SHAPES THAT CONTAIN PORTIONS OF A CIRCLE. FOR EXAMPLE, A QUARTER-CIRCLE COULD BE COMBINED WITH SOME STRAIGHT SIDES TO PRODUCE A MORE COMPLEX SHAPE. THEY COULD TRY TO MAKE THREE SHAPES, EACH INCLUDING AT LEAST ONE ARC OF A CIRCLE, SO THAT EACH SHAPE HAS A (DIFFERENT) TOTAL PERIMETER OF AS NEAR TO 12 AS POSSIBLE.
HOME LEARNING
Learners could extend this task by being asked to create three different quadrilaterals with different perimeters, but all as near to, say, 12 as possible. As well as drawing the shapes, they should show their calculation of the perimeter for each one.
About the expert
Colin Foster is a Senior Research Fellow in the School of Education at the University of Nottingham, and writes books for mathematics teachers (www.foster77.co.uk)









