CALCULATIONS WITH NEGATIVE NUMBERS ARE OFTEN CARRIED OUT BY FOLLOWING POORLY-GRASPED RULES, BUT ELECTRIC CHARGE PROVIDES A MEANINGFUL CONTEXT FOR UNDERSTANDING, SAYS COLIN FOSTER…

Lots of KS3 learners have heard that ‘two minuses make a plus’ but may not apply this rule correctly or have much sense of when or why it is the case. For example, some learners think that –5 – 3 = +8. In this lesson, links are made to the science topic of electricity to help learners understand adding and
subtracting directed (positive and negative) numbers.
STARTER ACTIVITY
Q Do you think that negative numbers exist? Why / why not?
Learners could discuss where they have come across negative numbers, such as with cold temperatures in Celsius. But does this mean they ‘exist’? Or are they just a human invention? Have they always been there ‘on the number line’, waiting to be discovered? People take different views and these questions might help learners to begin to develop their ‘philosophy of mathematics’.
Q Give me two positive whole numbers less than 10.
Whatever two numbers you are given you can use for the beginning activity. Below I have used 3 and 5.
Q If we let either or both of the two numbers be positive or negative, and we either add them or subtract them, either way round, what are all the addition and subtraction calculations we can make, just using each number once each time?
This is a bit complicated, so ask for learners to suggest a couple of examples first and put these on the board. Things like 3 – 3 are not allowed, because we are using each number only once each time. It may be helpful to show whether the number is positive or negative (e.g., with brackets) separately from whether the operation is add or subtract.
Learners will have to be careful and systematic to write down all the possibilities. For example, they could do all the additions and then all the subtractions, and by symmetry they should expect equal numbers of these. They could work on this in pairs.
There are two possibilities for the sign of each number, two ways round they can be written and two operations (add and subtract), giving 2 x 2 x 2 x 2 = 16 possibilities altogether:
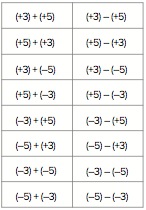
If learners are unsure whether they have found all the possibilities, ask them to see if they can find any more. They might become sure that there are no more because they have reasoned that there are 16 or because they have proceeded systematically and there are no more things to vary.
Q Which of these are easy to work out and which are hard? Why? Can you put them in order of difficulty. Don’t use calculators at this stage.
There are some very easy calculations here, provided that the positive signs don’t confuse. So 3 + 5, 5 + 3 and 5 – 3 are unlikely to present much difficulty. The order of difficulty of the others will depend on what methods the learners use. You could encourage them to colour red the ones they are completely unsure of, orange for the ones they are a little unsure of and green for the ones they are completely sure of.
At this stage it is best not to give any answers.
MAIN ACTIVITIES
1. Charges
If learners haven’t met before the idea of positive and negative charges, you could introduce this with some drawings, such as

QHow much do you think this is?
If some learners seem to get it and others don’t, ask those who do if they would not explain but instead give another drawing with the same value, such as
If no one has any idea, you could tell them that it is (+3), but don’t explain why. Then ask them another. They will quickly get the idea that one positive and one negative cancel each other out.
QNow I want you to make up pictures for the calculations and see which ones you can do. You probably won’t be able to do all of them yet. Just do the ones you can.
If you have small counters of two different colours (e.g., tiddlywinks) that could be useful; otherwise, learners can make dots with two different coloured pens.
All of the additions are easy and so are two of the subtractions. This includes (–5) – (–3), which, although it looks really complicated, when thought about with the charges is almost as easy as (+5) – (+3). However, the remaining six subtractions are hard, because what needs to be subtracted does not seem to be present!
INSERT IMAGE HERE
HOME LEARNING
Learners might be asked to try to explain the method to their parents/carers, who may not be familiar with it. They should not worry if their parents don’t immediately like it, as it is probably different from what they learned when they were at school!
2. The difficult ones There are six left that we don’t seem to be able to do. However, the drawings we made earlier can be used to do these. For example, we agreed that is 3.
So if we subtract (+5) from it, we get (–2).
Ask several learners to explain this until they are comfortable with it – it is quite hard!
This sorts out (+3) – (+5) = (–2).
QNow I want you to make drawings to do the remaining ones. This is hard, and learners are likely to need help. Some will want to write down the answers (maybe right, maybe wrong) without doing the drawings. You could ask them: How can you convince someone that your answer is right?
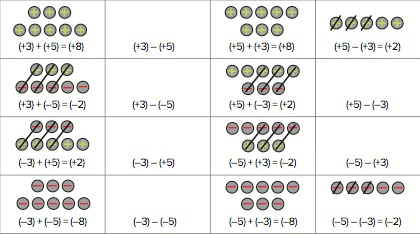
Learners could explain their diagrams to one another and make up others for the same calculations.
For a huge selection of free maths lesson plans for KS3 and KS4 click here.










